Jane Street gefur út mánaðarlegar þrautir sem er gaman að spreyta sig á. Fyrir utan það að vera ákveðin hugleiðsla, þá líkjast þrautirnar dagsdaglegri vinnu að því leyti að maður er alltaf að reyna að finna sniðugar lausnir á þeim vandamálum sem koma upp. Það er a.m.k. það sem ég segi sjálfum mér þegar ég sé fjölda klst. sem ég eyddi í þær.
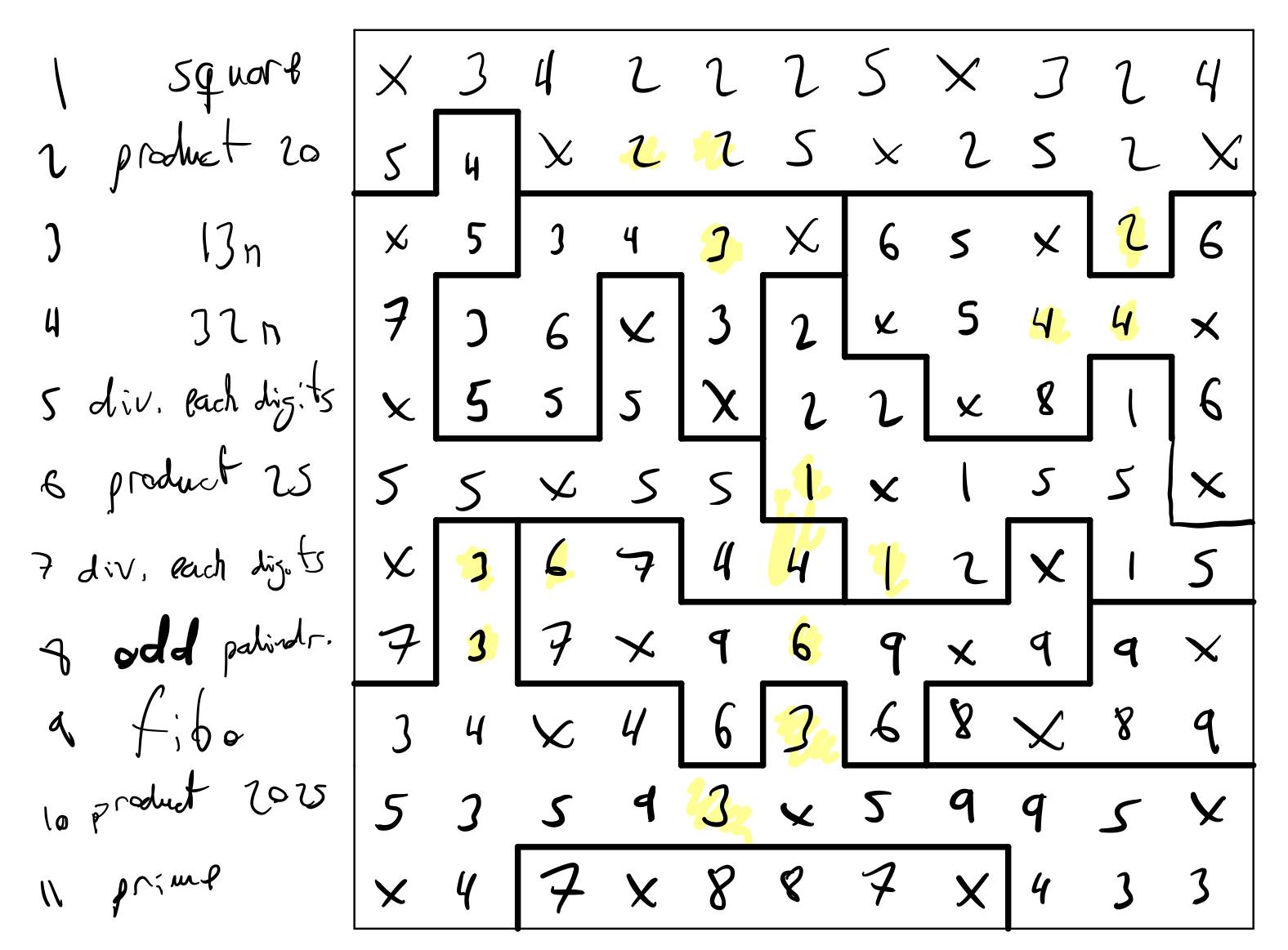
Þrautin fyrir maí mánuð lítur svona út
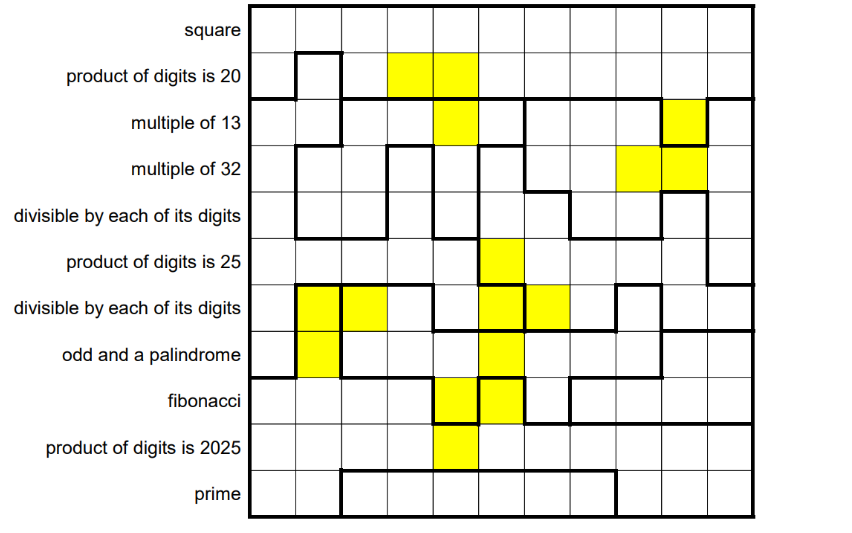
Maður byrjar með auða 11x11 grind. Þrautin snýst bæði um að finna tölustafi milli 1-9 til að setja í ólíku svæðin 9 og hellur til að skyggja á staka reiti. Hellurnar leyfa manni að dreifa gildinu sem var til staðar á aðliggjandi reiti. Gulu reitirnir hafa þann eiginleika að ekki má staðsetja hellu á þeim, og aðliggjandi hellum má ekki dreifa á gulu reitina. Tölurnar sem myndast á milli hellna innan hverrar raðar verða að uppfylla vísbendinguna sem gefin er vinstra megin við grindina. Reglurnar í heild sinni eru hér https://www.janestreet.com/puzzles/number-cross-5-index/.
Þetta er dæmi um þraut þar sem er erfitt að vera annað hvort einungis með blað og blýant eða einungis með tölvu. Það er ekki auðvelt að forrita lausn á þessu verkefni frá A-Ö, en líka erfitt að vera algjörlega án aðstoðar tölvu (t.d. til að finna allar tölur sem uppfylla vísbendingu tiltekinnar raðar). Ég skrifaði nokkur hjálparföll í Python til að leysa dæmið að hluta
find_candidates.pyfinna mengi allra kandídata í hverri röð fyrir siguse_candidates_single.pyfinna þær lausnir sem koma til greina fyrir gefna röð þar sem notandinn skilgreinir- upphaflega stöðu í röðinni (þ.e. án hellna)
- hvar í röðinni megi staðsetja hellur
- hve mikilli hliðrun megi gera ráð fyrir í röðinni fyrir ofan/neðan
use_candidates_multiple.pysameina lausnir úr 2) fyrir margar raðir, ásamt auka skorðum frá notanda (t.d. að röðimegi ekki innihalda hellu í sætij). Fallið skilar öllum mögulegum lausnum, ásamt mynd sem sýnir hvort að ákveðinn reitur innihalda alltaf/stundum hellu í sammengi lausnanna
Sjá meira um föllin hér: https://github.com/kjarripa/janestreet-may2025. Föllin eru skrifuð þannig að þau innihalda ekki alveg nægilega strangar reglur, t.d. gera föllin ráð fyrir því að aðliggjandi raðir mega innihalda 2 samliggjandi hellur. Föllin eru þó þannig að ef inntök notanda innihalda réttu lausnina, þá mun fallið líka skila henni.
Til að byrja einhvers staðar þarf að finna þær vísbendingar sem setja ströngustu kröfurnar. Allar vísbendingar með talnamargfeldi fækka verulega möguleikunum, ásamt því að setja skorður á tölustafina sjálfa. T.d. verður guli reiturinn í röð 6 að vera annað hvort 1 eða 5.
Ef við horfum á röð 2, þ.e. talnamargfeldi þeirra talna sem koma fyrir í röðinni er 20, þá getum við ályktað að efsta svæðið verður annað hvort að innihalda 1 eða 2 (20=2*2*5 og samliggjandi gulu reitirnir setja þessa skorðu). Við getum þá kallað í use_candidates_single.py fallið með eins litlum skorðum og hægt er fyrir röð 1. Með inntökunum að neðan getum við séð hvort til sé lausn á röð 1 ef efsta svæðið inniheldur töluna 1. Við setjum increment_from_above=0 því við erum að horfa á röð 1, og increment_from_below inniheldur 0 þar sem við á (getum aldrei sett hellur í sæti 2 eða 10 því tölurnar verða að innihalda a.m.k. 2 tölustafi).
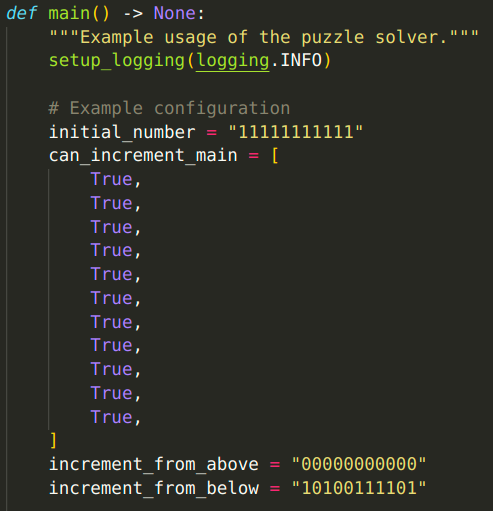
Þar sem fallið finnur enga löglega lausn fyrir eins litlar skorður og hægt er vitum við að efsta svæðið verður að innihalda töluna 2. Svona má halda áfram röð fyrir röð og enda með grindina